– Présentation
Un filtre passif permet de privilégier ou d’éliminer certaines fréquences du spectre d’un signal. Il s’agit d’un quadripôle linéaire.
Les filtres passifs sont des quadripôles constitués de résistances, de bobines et de condensateurs.
Le filtre est un quadripôle linéaire (2 bornes d’entrées, et 2 bornes de sorties), qui ne laisse passer que les signaux compris dans un domaine de fréquence limité, appelé la bande passante.
Les filtres permettent :
- d’éliminer des parasites, des bruits
- de sélectionner une fréquence, ou une bande de fréquence
Gabarit des filtres idéaux :
Le gabarit d’un filtre est en réalité la représentation du module de la transmittance en fonction
de la fréquence.
a) Le filtre passe bas :
Le filtre passe bas, comme son nom l’indique, ne laisse passer que les signaux ayant une fréquence inférieure ou égale à sa fréquence de coupure haute.
Sur le graphe représenté ci-contre, on voit que lorsque la fréquence est inférieure à la fréquence de coupure haute, la transmittance est égale à 1, ce qui signifie que la tension présente en sortie, est identique à celle présente en entrée.Si la fréquence est supérieure à la fréquence de coupure haute du filtre, la transmittance sera égale à 0, car la tension de sortie sera nulle.
b) Le filtre passe haut :
Le filtre passe haut, quand à lui, ne laisse passer que les signaux dont la fréquence est supérieur ou égale à la fréquence de coupure basse.Le raisonnement est analogue à celui que nous avons utilisé pour la
démonstration du filtre passe bas.
c) Le filtre passe-bande :
Le filtre passe bande, ne laisse passer que les signaux ayant une fréquence comprise entre la fréquence de coupure basse du filtre,et sa fréquence de coupure haute.
Ce dernier, est principalement utilisé dans les récepteurs radio. En effet, le filtre sélectionne une plage de fréquence plus ou moins étroite, correspondant à la plage de fréquence que nous voulons écouter sur notre récepteur.
d). Les filtres réels
Il est techniquement parlant, impossible de réaliser des filtres idéaux. Les filtres réels ne
possèdent pas des courbes de réponses idéal, et on ne peut définir les fréquences de coupure de
la même façon, c’est pourquoi nous allons les étudiés.
Les graphes ci-dessus, illustre bien, la différence entre les filtres idéaux, et les filtres réels.
Dans la suite du cours, nous allons nous intéresser uniquement aux filtres réels.
Notions de filtrage de fréquence
Fonction de transfert ou transmittance d’un quadripôle linéaire
Gain d’un quadripôle linéaire :
Il s’exprime en décibels (dB) et est définie par : G(f) = 20.logT
•Un filtre est caractérisé au moyen de deux représentations graphiques appelé diagramme de Bode :
- T module de la transmittance ou G le gain en fonction de la fréquence f,
- ϕdéphasage de la tension de sortie par rapport à la tension d’entrée, en fonction de la fréquence f.
•Bande passante à –3 dB d’un filtre passif :
la bande passante à – 3 dB est l’intervalle des fréquences pour lesquelles le gain G est supérieur ou égal à –3 dB.Elle correspond également à l’intervalle où le module de la fonction de transfert Test supérieur ou égal à 1/√2.
Propriétés de la fonction logarithmique :
1)Log(a * b) = log (a)+ log (b)
2)Log(a/b ) = log (a) - log (b)
3)Log(1/a ) = - log (a)
Le filtre passe bas :
Ce dernier peut se réaliser de moult manière, pour l’étude didactique, nous allons nous tourner
vers l’association d’une résistance et d’un condensateur.Nous avons sur ce schéma, une résistance et un condensateur.Afin de comprendre pourquoi ce filtre est passe-bas (il ne laisse passer les signaux ayant une fréquence inférieur à sa fréquence de coupure haute), nous allons faire une étude quantitative.
Pour faire cette étude, il faut savoir que l’impédance d’un condensateur est inversement
proportionnel à la fréquence. En haute fréquence, le condensateur se comporte comme un court-circuit, se qui va se traduire par une tension de sortie de 0V.
Étudions sa transmittance :
a) On applique simplement la formule de la transmittance :T = Us / Ue
b) On commence par exprimer Us :Par observation sur le schéma, nous voyons que nous pouvons utiliser le diviseur de tension, soit
c) On peut maintenant calculer la transmittance :
d) On remplace par les impédances et admittances, de la résistance et du condensateur :
On vient d’exprimer la transmittance. On exprime ensuite la transmittance sous la forme
élémentaire du filtre passe-bas. Cette formule est à admettre, et non à démontrer :
Nous pouvons faire l’analogie suivante :
Ce qui nous donne, pour Fo :
Module de la transmittance T :
On sait par définition, que pour un filtre passe bas, on a :
Si on veut le module, on a :
Et pour l’argument de T :
L’étude de notre filtre passe-bas, et ainsi achevé. Pour information complémentaire, nous allons étudier le comportement du filtre en fonction de la fréquence. Avant tout, un rappel des formules :
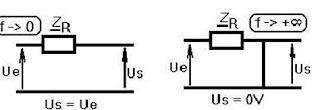
Quand F-> 0 :
Quand F = Fo :
|
Quand F -> l’infini
Détermination de la fréquence de coupure Fc :
|
La fréquence de coupure, est la fréquence pour laquelle on a :
G = G max – 3dB
Ainsi que :

Le filtre passe-haut passif:
1. Le montage :
3. Etude de la transmittance :
On utilise le diviseur de tension, car on a un filtre passif :
On remplace ensuite par les admittances et impédances :
On passe ensuite cette expression sous la forme élémentaire du filtre passe-haut :
Par identification, on a To = 1
Pour le calcul de Fo, il faut faire quelques lignes de calculs :
La fréquence « Fo », est identique pour un filtre passe-bas ou un filtre passe-haut.
3. Expression de la bande passante :
Comme son nom l’indique, ce filtre ne laisse passer que les signaux de fréquences hautes, sa bande passante sera donc :
4. Expression du module T :
On a trop souvent tendance, à faire l’erreur de laisser le « j » dans l’expression du module,
sachez que ce dernier n’est présent dans l’expression de T, que si le « T » est souligné.
Cette expression comporte un signe négatif devant le rapport « Fo / F », il ne faut pas l’oublier
en théorie. En pratique, on va faire une élévation au carré, ce qui aura pour conséquence de
neutraliser le signe négatif.
5. Expression du Gain G :
6. Expression du déphasage :






























Aucun commentaire:
Enregistrer un commentaire